Vorrei esprimere qui di seguito una serie di concetti di scienza delle costruzioni e tecnologia dei materiali, nel modo meno prolisso possibile e (spero) anche comprensibile ai più.
1) rottura duttile, rottura fragile e resilienza
I materiali, qualsiasi essi siano (sia da costruzione che per altri scopi), possono rompersi con due modalita, in modo duttile ed in modo fragile.
Le differenze:
- Fragile, improvvisa, superfici disgiunte lisce, nessun preavviso, a minore energia o con campo di resistenza limitato, allungamento del pezzo per la maggior parte impedito. Esempio pratico: la rottura di una lastra di vetro.
- Duttile: richiede tempo perché prima deve deformarsi (acciaio anche 20%, quindi una barra lunga 1 metro fa 20 cm), offre vistosi allungamenti che allertano sull'imminente rottura, crea una deformazione delle fibre del materiale che si irrigidiscono scorrendo fra di loro e in genere si verifica il fenomeno della strizione (esistono materiali non naturali che invece hanno un fenomeno opposto, ma possiamo trascurarli nel discorso). Esempio pratico: masticate una gomma e poi fra due dita tirate gli estremi...dopo qualche metro di allungamento si romperà in mezzo.
Come si passa da una rottura fragile ad una duttile? Per vari motivi, ma per noi i più importanti sono:
- temperatura
- urti improvvisi
L'urto abbassa la resistenza del materiale, che così può rompersi, assorbendo minore energia. Ciò è dovuto al fatto che non gli è dato modo di adattarsi e scaricare al meglio le forze o sollecitazioni interne e quindi reagisce al carico nel peggiore dei modi. Maggiore è la velocità dell'urto, minore è la capacità resistente del materiale.
Per definire quindi i materiali da costruzione viene eseguita una prova con un pendolo detto pendolo di Charpy, che misura al variare della temperatura quanta energia serva per portare a rottura un blocchetto del materiale opportunamente trattato.
Il grafico risultante si può vedere nella figura che segue
 A sinistra si ha l'energia, sotto la temperatura; la linea rappresenta, per un dato acciaio, l'energia utile per rompere con un urto un campione unitario di materiale ad una data temperatura.
A sinistra si ha l'energia, sotto la temperatura; la linea rappresenta, per un dato acciaio, l'energia utile per rompere con un urto un campione unitario di materiale ad una data temperatura.Nota storica: nel periodo della prima guerra mondiale veniva utilizzato acciaio dolce per la costruzione delle corazzate. Potete notare che intorno a 0°C l'energia per la rottura fragile fa un salto notevole. La rottura di molte corazzate squarciate da parte a parte in giorni d'inaugurazione piuttosto freddi, per mezzo della classica bottiglia lanciata contro la nave, spinse gli studiosi ad approfondire questo fenomeno, la resilienza dei materiali.
Quello che si può capire da questi concetti è che materiali durissimi, creati per sostenere migliaia di tonnellate di peso o di sollecitazioni, al variare della temperatura devono fare i conti con un altro problema, la resilienza.
Questo fenomeno porta a ridurre enormemente l'energia utile per distruggere i legami degli elementi costituenti l'edificio, poiché nei fenomeni in cui una parte di questo urta quella che sta sotto, magari compiendo un salto di un solo piano (3,5 metri in genere), il materiale non ha modo di allungarsi per l'impatto improvviso e non ha modo di adattarsi. E' come prendere un sollevatore di pesi e lasciare che sollevi 200 Kg o buttargli addosso di scatto 200 Kg senza che se l'aspetti.
Gli acciai utilizzati per le costruzioni, inoltre, non sono i dolci o gli extradolci (quelli che tendono alla ghisa, che hanno maggiori quantità di carbonio) ma sono i duri. Ciò è fatto appositamente, poiché è più sconveniente un acciaio che a 0°C ha quel salto di energia di rottura visibile che uno duro più diluito e che non modifica il suo comportamento lavorando nel campo delle temperature dell'ambiente.
Noterete comunque che la resistenza agli urti per unità di superficie di impatto anche nel caso maggiore non supera i 350J: ben distante dalle resistenze che possono essere offerte quando si lavora in campo statico (in altre parole si appoggia il carico progressivamente).
2) instabilità dell'equilibrio
Di instabilità dell'equilibrio esistono fondalmentalmente tre specie; la trattazione è complessa per ognuna di essa e difficile da eseguire in un blog. L'unica cosa che posso fare quindi è farvi provare una delle tre possibili instabilità di cui può soffrire una struttura metallica. Serve una molla, una di quelle delle penne va benissimo (occhio che rischiate di perderla). La molla rappresenta la vostra colonna. Il dito rappresenta la forza peso di ciò che sta sopra la colonna.
Immaginiamo per esempio di caricare un piano, un solaio che poggia su quattro colonne. Un quarto del peso si scarica su una di queste colonne (quel peso è il vostro dito). Prendete la molla, appoggiatela sul tavolo e sfioratela col dito. Ora cominciate a caricare la molla, gradualmente e man mano che la caricate avrete che essa si contrae sempre di più.
Sapete benissimo che la molla segue la legge: F=K*U
dove K è una costante chiamata rigidezza, U lo spostamento di contrazione della molla e F la forza che vi applicate.
Voi aumentate di poco la F che vi applicate col dito e vi aspettate che la contrazione della molla sia piccola in proporzione con K (come da relazione ndr). In realtà alcuni di voi (pochi) avranno la fortuna di aumentare la forza e contrarre la molla finché questa si trova con tutte le spire aderenti; gli altri avranno per un tratto un comportamento sopra descritto... poi di punto in bianco la molla schizzerà via da qualche parte (la perderete) e il carico (il vostro dito) si reggerà sul nulla (l'aria, perché la molla è schizzata via).
Questo secondo comportamento è dovuto all'instabilità dell'equilibrio ed è estremamente dannoso, poiché toglie un vincolo alla struttura e la forza peso deve essere ridistribuita ad altri elementi per essere sorretta.
Per coloro ai quali l'instabilità non si verifica, prendete una molla + lunga e riprovate (avrete per un certo rapporto K/l che si verificherà l'instabilità dell'equilibrio).
Da cosa dipende l'instabilità dell'equilibrio? Nella trattazione classica (la trattazione ottima è usare il metodo omega) usata fino a 10-20 anni fa, l'instabilità dell'equilibrio di prima specie è, secondo la trattazione euleriana, direttamente proporzionale alla rigidezza (K=EJ, E modulo elastico e J momento di inerzia della sezione di sbandamento minima) e inversamente proporzionale al quadrato della lunghezza libera di inflessione (immaginate nell'esempio precedente che la lunghezza libera di inflessione era la lunghezza della molla, in realtà nel caso strutturale il discorso si complica secondo i vincoli di attacco delle colonne, ma il fattore di cambiamento è solo un coefficiente numerico fisso).
Quando nel WTC sentite parlare di travi orizzontali usate per chiudere gli sforzi, in realtà quelle non sono altro che un accorgimento per ridurre la lunghezza libera di inflessione, poiché irrigidiscono la struttura (creando problemi e stati di sollecitazione interna se per il calore questi elementi irrigiditi devono allungarsi).
Quando la ricostruzione tecnica comunemente accettata valuta che è crollata una serie di solai-pavimenti, la mancanza di quegli elementi lascia sempre più porzioni di colonna libere di inflettersi (è come se la molla divenisse sempre più lunga e l'instabilità dell'equilibrio aumentasse...).
Quindi abbiamo la definizione di carico critico euleriano: sempre riprendendo l'esempio precedente, per un carico inferiore a quello per cui la molla arriverebbe a essere tutta contratta (snervata o rotta), la molla schizza via istantaneamente (perde la connotazione di piccoli gradienti e piccoli spostamenti), creando una situazione di pericolo notevole non prevista se si costruisse soltanto badando al carico di rottura della colonna.
E' per questo che una verifica all'instabilità dell'equilibrio è un obbligo previsto dalle normative di tutto il mondo, come ogni buon ingegnere vi saprà dire, al contrario di filmografi, teologi e filosofi.
A ciò si aggiungono un'altra serie di problematiche la cui trattazione diviene veramente complessa... soprattutto per i blog.
1) La mancanza di una fila di colonne crea una ridistribuzione delle forze ed un momento (Jones parla di momento torcente... in realtà è un semplice momento flettente con compressione, quindi pressoflessione; il momento torcente è uno solo ed avrebbe fatto ruotare il WTC sul suo asse verticale al terreno) che rende molto più probabile la formazione di instabilità dell'equilibrio (e anche di raggiungere il carico critico di compressione delle colonne d'angolo). Secondo l'esempio con la molla diviene un po' difficile ricrearlo, dovreste avere la molla ed il dito collegati, premere e ruotare lievemente il dito insieme. Noterete che sbanda prima da un lato.
2)Un fuoco che brucia cede calore alle colonne. Il comportamento delle colonne in acciaio rispetto al fuoco verrà in seguito descritto. Ha un punto critico a 550°C per cui varia notevolmente il comportamento. Variano inoltre le caratteristiche resistenziali della colonna (si rompe prima per valori di carico più bassi). Insomma non deve per forze esserci la liquefazione della colonna a 2200°C perchè questa ceda, basta solo combinare più cause per farla cedere. All'atto pratico diciamo che il calore abbassa il molulo elastico E, e il carico critico di instabilità è proporzionale a E*J...quindi sarà sempre minore, quando invece le colonne hanno subito maggior carico.
Tutte queste cause messe insieme fanno due comportamenti ben distinti per le due torri.
Il primo comportamento è stato con tutte le colonne che al medesimo istante han ceduto di botto, crollo inizialmente verticale fino all'urto piano con piano.
Il secondo invece ha previsto una leggera rotazione.
La rotazione è ovviamente dovuta ad un momento non contrastato, cioè delle colonne che hanno ceduto prima di altre.
Il motivo per cui delle colonne cedono prima di altre è che quelle colonne, prossime al punto di impatto, alla breccia erano maggiormemente sollecitate a peso dei piani superiori ed a momento flettente. Il calore ledeva le caratteristiche resistenziali dell'acciaio ed abbassava il carico di snervamento.
Raggiunto il carico di snervamento il comportamento è divenuto di scorrimento ed il carico residuo è finito alle rimanenti colonne, che si son trovate nella medesima situazione delle precedenti...
Così il crollo è progredito facendo ruotare l'ammasso superiore di piani.
Il comportamento dell’acciaio al fuoco ha una stretta dipendenza dalla temperatura raggiunta e dai fenomeni chimici che variano la sua struttura chimica.
Limitando il discorso ai punti più interessanti per il blog dobbiamo considerare alcuni aspetti peculiari del comportamento dell’acciaio al calore con conseguenze nella stabilità dell’edificio: allungamento-collegamenti, allungamento impedito, proprietà meccaniche-calore. Primo fra tutti viene l’allungamento o la dilatazione dovuta al surriscaldamento del materiale.
Per semplicità cito la formula dell’allungamento del materiale nell’intorno della temperatura ambiente e non sotto sforzo (o carico), la cui valutazione è di diversa natura.
In questo caso la formula per valutare la dilatazione del materiale è:
deltal=alfa*L*deltaT
deltaT è la variazione di temperatura
deltaL è la variazione di lunghezza
L è la lunghezza della barra di acciaio presa in considerazione
Alfa è una costante termica pari a 0.000012 (per temperature nell’intorno di 24 °C)
Per una lunghezza di 3,5 metri, una variazione termica di 100°C (se poi la temperatura dovesse risultare di 600 basta moltiplicare per 6 il deltaL) risulta un allungamento di: 0.0042 metri, cioè 4,2 millimetri.
Immaginiamo per esempio di avere due colonne di acciaio legate con una chiodatura fra le due.
Una si dilata di 4 millimetri perché sottoposta a calore, l’altra non si dilata. Abbiamo che il chiodo di collegamento viene da un lato a restare fermo, dall’altro a doversi spostare magari tanto quando il suo raggio (5 millimetri).
Questo si intuisce facilmente ha delle conseguenze sul collegamento fra le due colonne.
- Altro aspetto da non trascurare è che l’allungamento delle colonne è impedito. In altre parole il carico di piani superiori a colonne che subiscono la dilatazione termica viene a schiacciare quelle sottostanti rendendo più semplice per la colonna allungarsi flettendosi piuttosto che restando rettilinea.
Questo tipo di sbandamento previsto nel caso di verifica antincendio della struttura (anche se è da valutare come nel progetto dell’edificio e con che normativa), assume molta importanza nel caso dell’instabilità dell’equilibrio, poiché abbassa il carico critico di formazione dell’instabilità (in altre parole per carichi che diventano minori si rischia di avere instabilità dell’equilibrio e quindi di avere uno sbandamento istantaneo della colonna compressa).
- Per quanto riguarda il comportamento delle caratteristiche del materiale, riutilizzo i grafici del NIST (link).
Il modello preso in considerazione per valutare il collasso considera soltanto 5 piani del WTC1 della facciata nord dell’edificio (differentemente dal modello di Usmani del 2003 che considerava 12 piani).
The principal reason for including only five floors in the analysis is to have the simplest model that will still capture salient features of the collapse of the towers.
Insomma meno elementi nel modello permette una migliore cura di quelli presenti visto il limite delle capacità computazionali verso cui ogni programma di calcolo si scontra.
The fire applied to the model only heats two floors, and the remaining floors remain cool and provide lateral restraint to the perimeter column under study.
Il fuoco invece che a tre piani (ma da foto e testimonianze appare evidente che si era diffuso anche in altri piani) viene applicato a due piani ed agli altri non vi si applicano sbalzi termici.
The various steels range in nominal yield strength from 250 MPa (36 ksi) in the floor trusses to 450 MPa (65 ksi) in the column (McAllister 2002). They are all modeled by bilinear stress-strain curves, with a tangent modulus about 0.5 percent of the elastic modulus. Figures M–1 and M–2 show the steel properties for the temperature range used in the analysis. Usmani et al. (2003) used similar steel properties.
Nella travatura reticolare del pavimento è stato utilizzato in acciaio con capacità di snervamento di 250 Mpa (36 ksi) nelle colonne un 450 MPa (65 ksi) come definito dal McAllister 2002.
La loro modellazione non lineare segue delle curve stress-strain come da seguenti figure (M1 e M2) con un modulo elastico tangenziale approssimativamente dello 0.5% del modulo elastico.
Usmani (2003) ha usato materiali dalle proprietà simili.
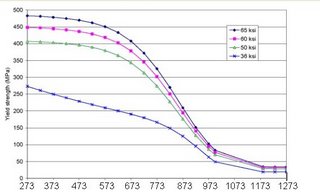
A sinistra abbiamo sulle ordinate la forza a cui può resistere l’acciaio a snervamento.
I colori diversi sono i vari tipi di acciaio, a noi interessa quello blu, il 36ksi (all’incirca l’italiano Fe360) e il blu scuro il 65Ksi.
Tutti gli acciai intorno ai 773 °C hanno un forte abbattimento della capacità portante di snervamento... in altre parole il loro carico che riescono a sopportare senza finire in zona plastica si riduce considerevolmente, soprattutto per gli elementi che costituiscono la travatura reticolare del solaio con 36ksi.
In effetti il modello di crollo previsto dalla teoria ufficiale parla di cedimento dei solai con sbandamento di questi a cui segue il cedimento delle colonne.

Nel grafico seguente viene mostrato invece di quanto cala all’aumentare della temperatura il modulo elastico.
Per capire meglio, ripensiamo alla molla, lo Yield strength (o stress o sigma) rappresenta la forza con cui premiamo su questa, la epsilon o strain rappresenta lo spostamento e il modulo elastico E rappresenta la costante elastica della molla (K).
F=K*u ---> sigma = E* epsilon
La similitudine comportamento della molla - comportamento della colonna con solo sforzo assiale è piuttosto comune.
Maggiore è la costante elastica maggiore è la forza che dobbiamo mettere per comprimere le spire della molla, in altre parole maggiore è il carico che la molla riesce a sostenere a parità di spostamento o la capacità portante della colonna.
Quello che non si percepisce da questi grafici del NIST è la variazione della capacità di lavoro che può essere offerta dalla colonna, poiché quelli presentati sono dati (sigma e modulo elastico o di Young) da inserire nel programma di calcolo per descrivere le modalità di comportamento del materiale componente la struttura.
Così le variazioni rappresentate sembrano in effetti poca cosa nell’intorno dei 500-600°C, poiché si analizza il comportamento dei fattori caratteristici delle proprietà dei materiali separatamente.
Il lavoro di un elemento di acciaio invece è rappresentato dalla prodotto della sigma per la epsilon (stress e strain), in altre parole nella curva che segue

tratta da qui, in cui si analizza il comportamento di una travatura reticolare sottoposta a calore.
Non è altro che l’area sottostante alle curve per un dato punto della curva che rappresenta lo stato di sollecitazione della colonna.
Si vede quindi che la capacità di eseguire lavoro per resistere alle sollecitazioni cala drasticamente con la temperatura, poiché le caratteristiche resistenziali a subire gli effetti della temperatura sono due (abbassamento della sigma di snervamento e abbassamento del modulo elastico-tangenziale).
Queste variazioni del comportamento del materiale incidono sue tre aspetti strutturali: l’instabilità dell’equilibrio, variazione delle tensioni interne massima raggiungibili o di snervamento, ridistribuzione delle tensioni in funzione delle nuove rigidezze.
Più in dettaglio abbiamo che:
All’instabilità dell’equilibrio come già detto non giova una variazione delle caratteristiche statiche e delle proprietà dei materiali presi in considerazione.
Utilizzando la trattazione di Eulero, il carico di instabilità critico cala con il modulo elastico.
Il grafico del modulo elastico o di Young, sopra riportato, indica una riduzione di un terzo del suo valore per una temperatura di 700 °C, quindi di conseguenza il carico per cui può esserci instabilità dell’equilibrio diviene di un terzo più piccolo per tutte le colonne coinvolte nell’incendio secondo quella data temperatura.
La variazione delle tensioni di snervamento o di rottura riduce la capacità resistente della trave-colonna, che si trova così ad avere minor lasco di sicurezza rispetto a quanto previsto progettualmente.
Le colonne vengono infatti progettate per azioni massime permanenti e variabili (incendio e aereo sono azioni eccezionali diverse da permanenti e variabili) a snervamento.
Ciò permette di avere un lasco di capacità di lavoro della colonna in campo plastico di sicurezza.
Però l’affievolimento delle capacità portanti del materiale riduce le resistenze e un’azione eccezionale quale un aereo che strappa parte delle colonne aumenta le azioni sul resto delle colonne.
Abbiamo quindi che rispetto le situazioni ordinarie le resistenze calano e tendono alle azioni che aumentano….in altre parole non tendiamo alla sicurezza strutturale.
La valutazione della differenza fra resistenze ed azioni (permanenti ed accidentali-variabili) è di difficile computo, spesso anche attraverso un programma di calcolo (il quale dovrebbe considerare non solo i dati esatti di inizio fenomeno, ma anche la storia di carico precedente al fenomeno crollo).
La variazione del modulo elastico non solo diminuisce il carico critico di instabilità, ma varia le rigidezze degli elementi strutturali.
Ciò non aumenta le azioni né le diminuisce... ciò semplicemente ridistribuisce le tensioni all’interno della struttura secondo il bilancio delle rigidezze, dando maggiori tensioni agli elementi con maggiore rigidezza e togliendono parte a quelli con minore.
Per capire meglio, prendendo un piano e appoggiando ai 4 vertici 4 colonne di eguale forma rigidezza, le forze si ripartiscono su questi 4 elementi uguali…quindi ogni colonna porta un quarto del peso.
Se una colonna per qualche motivo si rammollisce, rimangono tre colonne, la struttura entro certi limiti si regge ancora in piedi, ma una colonna non porta più carico, quindi le tre colonne nella variazione di capacità portante passeranno da un quarto a un terzo.
Se avessero avuto differenti rigidezze (magari perché non tutte esposte al fuoco…o esposte a temperatura minori) ciò avrebbe comportato che quella più rigida avrebbe portato maggior carico rispetto alle altre.
Ne deriva che se su 4 colonne a rigidezza variabile una viene a mancare, la ridistribuzione del quarto sopra accennato tenderà a aumentare più di un terzo il carico sulla colonna più rigida, mentre le altre avranno meno del terzo prima indicato.
Un esempio forse più chiaro è il classico del tirare il carretto:
Prendete un carrettino, lo caricate, e mettete ai due bordi in cui lo volete tirare un elastico da una parte e una corda dall’altra.
Prendete in mano i due estremi e tirate (applicate una tensione di trazione ad entrambi gli estremi).
L’elastico si allunga e non sposta il bordo a cui è legato, la corda non si allunga perché ha maggiore rigidezza assiale rispetto all’elastico, quindi il bordo della corda si sposta ed essendo legato ad un solo lato il carretto tenderà a curvare.
Nel caso delle colonne e della forza peso si ha lo stesso fenomeno. Questo gioca a sfavore della sicurezza, poiché nel caso di incendio il modulo delle colonne esposte a temperature maggiori cala ridistribuendo i carichi verso le colonne più fredde. Ovviamente questa ridistribuzione potrebbe essere la goccia che fa traboccare il vaso.
Chiudendo un discorso che potrebbe essere molto più lungo parlando di variazioni normative chiodature e modelli di approssimazione degli eventi fisici, questi concetti sono difficili da applicare a mano per verificare se da dati effetti si riesce a risalire in modo del tutto certo e unico a quella causa scatenante.
Il modo migliore visionare un fenomeno come quello del 911 è per mezzo dei programmi di calcolo.
Questi concetti servono per avere un’idea di come tendono ad evolversi i fenomeni di quel genere e permettono un miglior controllo dei dati in uscita dei programmi di calcolo (può sempre capitare errore umano nella meshatura).
Sono concetti base dell’insegnamento con cui ogni progettista deve fare i conti prima di mettersi a ideare un qualsiasi edificio. Non si spiega come mai in 5 anni nessun filantropo, teologo, filosofo ecc…non abbia voluto citarli intervenendo comunque nell'argomento 11 settembre 2001.
Non abbiamo quindi le colonne che crollano solo se fondono... piani di decine di migliaia di tonnellate che si mettono in moto e dovevano fermarsi subito al primo solaio... e tante altre voci simili, facili da immaginare ma dissociate dalla realtà costruttiva che hanno ispirato sentimenti ai fruitori di disinformazione, ma abbiamo una situazione più complessa la cui valutazione risulta difficile anche in qualche migliaio di pagine di rapporto (riferimento al rapporto NIST).

Nessun commento:
Posta un commento